The Golden Ratio is most simply described as the ratio created in the situation below.
Math
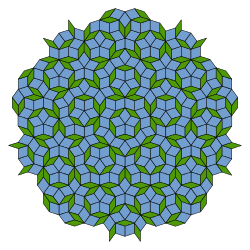
A penrose tiling
The Golden Ratio is the basis for many shapes in math, including the Golden Rectangle, the Golden Triangle, the Golden Spiral, and Johannes Kepler's Kepler Triangle. It is also the basis for the construction of pentagons and dodecahedrons.
The Golden Ratio also allowed for the discovery of Penrose Tiling and quasicrystals in the 1980's, a new form of matter. This was a huge contribution to the world of science and math.
Also, the symbol of the Pythagorean brotherhood was a pentagram, directly related to Phi.
The Golden Ratio also allowed for the discovery of Penrose Tiling and quasicrystals in the 1980's, a new form of matter. This was a huge contribution to the world of science and math.
Also, the symbol of the Pythagorean brotherhood was a pentagram, directly related to Phi.
5
Phi is directly based on the number 5.
Φ = (square root of 5 + 1)/2
Φ = 5^.5 x .5 + .5
Φ = square root (5 + square root of 5 / 5 - square root of 5)
Φ = (square root of 5 + 1)/2
Φ = 5^.5 x .5 + .5
Φ = square root (5 + square root of 5 / 5 - square root of 5)

